算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

青山学院中入試対策・算数の合否を分けた一題（2020年度）

難易度分類

１	A
２	A
３	A
４	B
５	A
６	A
７	A
８	B
９	B
１０	B
１１	A
１２	B
１３	C
１４	C

A…青山学院中等部合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

総評

青山学院中等部の出題傾向は、いくつか特徴があります。旅人算や平均に関する問題が出やすいなど、過去問に取り組んでいる中で、その頻出分野に気づくことでしょう。
問題数が多い試験構成になっているため、手際よく問題を解き進めることが求められます。
日ごろから多くの問題に触れ、基本的パターンをすぐに引き出せるよう頭の中を整理しておきましょう。

問題別寸評

大問4

縮尺と降雨量の問題です。
過去の類題としては、2019年の大問5など。一見異なる問題のように思えますが、根本原理の「１当たりの量」というテーマという点で共通しています。
3.5×2500×2500×0.2÷500＝8750　です。

大問5

２つのグループがあり、それぞれに所属している人数などに関する問題は、線分図・表・ベン図の３つが代表的な考え方です。
今回はこの中でベン図を用いるのが良いでしょう。
青山学院中等部は割合に関する問題を非常に多く出題する学校であり、必然的にこうした問題が再度出題されることは十分考えられます。
2020年度入試はベン図でしたが、表で整理する問題なども練習しておきましょう。

大問6

青山学院中等部は、やり取り算や相当算に該当する問題をここ数年毎年出題しています（2019年大問6や2019年大問6、2018年大問7など）。
今年もその流れは変わらず、本問で出題されました。
やりとりの流れを表す図を描いて、ミスを防ぎましょう。

大問7

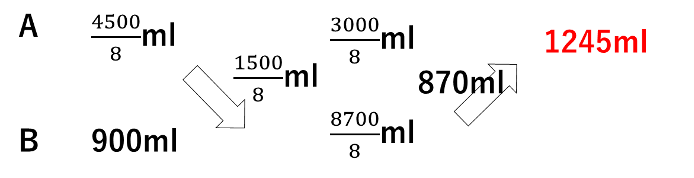
旅人算の問題です。旅人算も、青山学院中等部で非常に頻出の単元です。
特に、時間や距離、速さの一定に注目して比を利用するタイプの問題が多く出題されています。
後半の大問で重たい問題が出題されることもあれば、2020年のように、中頃の大問で出題されることもあります。
【旅人算の問題】
2019年大問9
2018年大問14
2017年大問14
上記のように、旅人算の問題はここ数年毎年出題されています。
細かく見ていくと、問題文はそれほど長くはなく、3～4行程度です。
通過算、流水算、往復の旅人算など出題テーマは多彩です。
時間や速さの一定に注目して、比を用いて答えに近づいていくプロセスは共通していることが多いです。塾のテキストに掲載されている旅人算の問題を多く解き、自分の中にパターンのストックを多く持つようにしましょう。

本問は、線分図（状況図）が丁寧に書ければ分かりやすいでしょう。
青山学院中等部は、ダイヤグラムの作図までを要求する問題はまれです。線分図（状況図）のポイントを押さえて書くことができれば解決の糸口をつかめる問題がほとんどです。
「同じ時刻のポイントに同時刻マークを書き入れる」などの基本動作を繰り返し定着させましょう。

大問8

平均を利用した割合の問題です。
【平均を利用する問題】
2019年大問11
2018年大問9
2017年大問6

中学入試において「平均」が出題されたならば、即座に「合計」を求めることが定石です。つまり、平均点に人数を掛け算します。しかし、この問題では具体的な人数が示されておらず、代わりに「女子の人数は全体の64%です」のように示されています。問題文中に一か所だけ「5人」という人数の情報が書かれていますので、ここと関連させて全体の人数を求めることが最初の目的とすべきことです。

割合の問題では「具体的な数が分かっているのか・分かっていないのか」や「計算すれば具体的な数を求められるのか・割合の数字のまま計算するしかないのか」などを判断する必要があります。
その問題が、どのような位置づけの問題なのか判断できるようになると、こうした問題が得意になるでしょう。

本問は、平均の問題と割合の問題を単純に合体させたような構成になっています。
「はじめ女子の人数の割合は64％でしたが、男子が4人増えたので女子の割合は60％になりました。初め男女はそれぞれ何人だったでしょう」　→答え：女子48人、男子27人
という問題と
「75人のクラスの平均点は68点で、女子48人の平均点は71.5点です。男子27人の合計点は何点でしょう」　→答え：1668点
という問題と
「男子27人の合計点が1668点、欠席していた男子5人の平均点が66.4点でした。男子32人全体の平均点は何点でしょうか」
という3つの問題を単純につなぎ合わせただけの構成です。
ひとつひとつの問題は難しくありませんが、実際の問題文はこの3段階のそれぞれに必要な情報が区別なく書かれています。
まずは問題がどのような構成になっているのか、最初の一手はどの数字を使って計算するのか。
ここの判断力が問われた問題でした。

大問9

エスカレーターの問題です。
類題として動く歩道の問題は2016年の大問14で出題されています。

歩数・歩幅の問題は、苦手意識を持っている生徒が多いように思えます。
特にエスカレーターの問題は接する回数が少ないため、ある程度の慣れが必要です。

しかし、問題の本質としては流水算と変わりありません。
問題文の「段」を「メートル」に読み替えると分かりやすくなります。

例えば、「兄が5段歩いて上がる間に弟は3段歩いて上がる」は「兄と弟の静水時の速さの比は5:3です」と同じ意味です。
「兄は50段、弟は40段歩いたところで改札のある階に着きました」から、兄と弟のかかった時間の比を求めます。すると、3:4と分かります。
また、同じく「兄は50段、弟は40段歩いたところで改札のある階に着きました」という部分から、自力で歩いた距離の差が10段分となります。言い換えると「エスカレーターに運んでもらった距離」が10段分です。

エスカレーターは一定の速さで動き続けていますので、兄と弟がエスカレーターに乗っていた時間の比である3:4の差の1の時間で、10段動いたことが分かります。
よって、兄は30段、弟は40段分エスカレーターに運んでもらっていますので、答は80段となります。

大問10

キャンディーを混ぜた際の値段を求める問題です。
こちらは、問題の本質としては食塩水の濃度を求める問題と同じになります。
「100g当たりいくら」のように、単位量当たりの値段などを問う問題は青山学院中等部では特徴的によく出題されます。
一回の入試問題につき割合の問題がいくつも出題されますが、どれも性格が少しずつ異なる問題です。「割合」や「比」について、多角的に理解していることが求められます。
本問は本質的には食塩水と同じですので、解法も同じものを使うことができます。つまり、面積図やてんびん図が使えます。これらの図の意味について機械的に暗記ではなく、意味まで深く理解していることが求められます。そうでないと、本問のように「キャンディーの値段」と外側を変えられただけで混乱してしまうかもしれません。

大問9のエスカレーターの問題でも、「段」を「メートル」に読み替えると理解しやすかったですし、本問もキャンディーの値段を食塩水に読み替えると理解しやすいです。このように、表面上の表現を変えた出題をすることがあります。
これは、「問題の本質を理解できているか、表面を変えられただけで混乱したりしないか」という点を試しているのだと思います。
しっかりと根本から理解できるように学習しましょう。

大問11

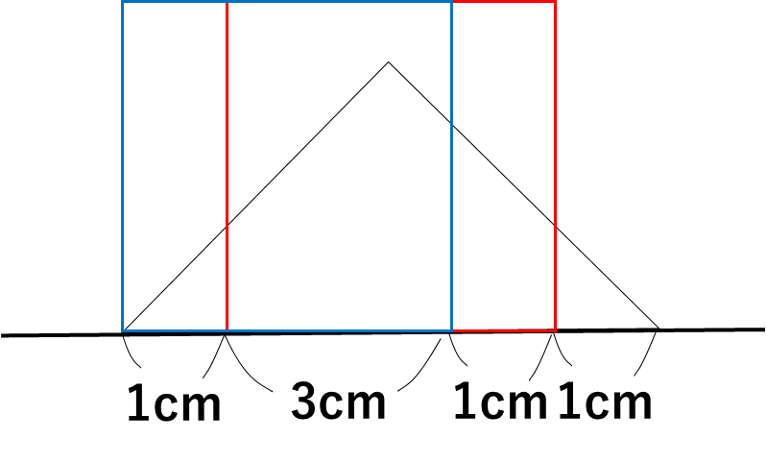
図形の移動に関する問題です。
下のような図を簡単に作図し、面積を求めます。
直角三角形アの面積から、左右二つの直角三角形の面積を引くという方針さえ見つかれば、さほど難しくはない問題だったでしょう。

大問12

円を折り返した図形の面積を求める問題です。
ほぼ同じ問題が、大手塾のテキストにも掲載されています。
円を含んだ部分の面積を求める際には「曲線に両端と円の中心を結ぶ補助線を引く」が常套手段です。しかし本問の場合は折り返しているため、折り返しの線と線対称の位置に、仮想の中心を設定することがコツです。すると、正三角形を見つけることができます。

問題13
水そうに水を入れる問題です。
「容器に水を入れる」という問題はここ数年でよく出題されています。
2019年大問8
2018年大問11
2017年大問13

などです。使用する解法や根本原理にはばらつきがあり、底面積の比を利用する問題や、重りを入れる問題が過去に出題されていましたが、今年は容器の向きを変える問題です。
2020年度の出題はどちらかというと、立体図形の体積を求める問題や、相似を利用して長さを求める問題の要素が強くなっています。

このような問題については「水の体積が変わらない」ことを利用し、各部分の体積を求めていきます。
（1）であれば、図1より水の体積は　10×10×13.7＝1370㎤と求められます。
また、図2の左方面、直方体の部分については　10×20×6＝1200と求められます。
1370－1200＝170より、図2の右側の三角形の部分に入っている水が170㎤と求められるため、ここから答えを求めていきます。
このように、立体を部分に分割する考え方を用いる問題でした。

（2）のほうが簡単だったかもしれません。水が入っている部分の立体図形は、三角柱+台形柱　です。三角柱の方の体積は　5×10÷2×10＝250㎤と求められますので、後は簡単でしょう。

合否を分けた一題

大問14

「全体を部分に切り分ける」という発想を使うという点で、大問13の容器に水を入れる問題と共通しています。パンの種類ごとの合計金額、また表2の使った金額ごとの合計金額など、2種類の切り分け方を使います。
一見すると全く別の問題ですが、着眼点は似ています。

また、「人数を掛け算することで合計を求めてから考える」という点では、平均の問題と似た着眼点となっています。平均の問題は青山学院中等部で頻出ですので、きちんと意識して過去問に取り組んでいた受験生ならば、本問についても解法が思いつきやすかったのではないでしょうか。

問題文に示されている表の左又は右に、下のような情報を書き加えます。この種の問題でのよくある手段ですので、必ず習得し使えるようになっておきましょう。

上のようにして、各金額で、それぞれどのパンを買われているのかを一覧にします。
250円の時は、250円のカレーパンを1個買っている場合と、100円のあんパンと150円のクリームパンの2個を買っている場合の2通りあることに注意しましょう。
今後説明のため、250円使った生徒のうち、カレーパン1個の人数をAとし、あんパンとクリームパンの2個を買った生徒の人数をBとすることにします。（A+B＝40です）

さて、あんパンを買った生徒は
26+B+【350円の人数】+8＝57
クリームパンを買った生徒は
32+B+【400円の人数】+8＝80
となります。
問題で聞かれているのは【350円の人数】と【400円の人数】の差ですので
（80－57）－（32‐26）＝17人
より答えは17人となります。

（2）
売れたパンの金額の総額から考えていきます（平均算の際に合計点を求めることと似た発想です）。
100×57+150×80+250×75＝36450円
次に、下の表のように、人数が分かっている項目の金額を求めていきます。

よって
2600+4800+10000+4000＝21400

このふたつの金額の差を求めると
36450－21400＝15050円
これが、350円と400円の項目の合計金額です。
(1)で、この2項目の人数の差が17人だと求められていますので、
（15050－17×400）÷（400+350）＝11
よって350円が11人、400円が28人です。

したがってカレーパン1個を買った生徒の人数は、
75－（11+27+8）＝29
より29人です。

総評

割合に関する問題は、例年の傾向を踏襲していました。やはりこうした問題については、こだわりを持って出題しているようです。
一方で、割合以外の問題、平面図形や立体図形については、必ずしもここ数年の傾向通りではない問題も出題されています。
割合については、直前期には過去問を通じて頻出パターンをトレーニングすることが肝要です。
一方で、それ以外の単元についても各塾のテキストをしっかり復習するなどして、幅広い問題に対応する力を身に着けるべきです。直前期だからと言って過去問演習ばかりではなく、塾のテキストや併願校の過去問などを通じて、幅広い単元の学習が必要です。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？