算数の合否を分けた一題
青山学院中入試対策・算数の合否を分けた一題（2016年度）
難易度分類
| ［１］ | Ａ |
|---|---|
| ［２］ | Ａ |
| ［３］ | Ａ |
| ［４］ | Ａ |
| ［５］ | Ｂ |
| ［６］ | Ｂ |
| ［７］ | Ｂ |
| ［８］ | Ｂ |
| ［９］ | Ｂ |
| ［１０］ | Ａ |
| ［１１］ | Ｃ |
| ［１２］ | Ｂ |
| ［１３］ | Ｂ |
| ［１４］ | Ｃ |
A…青山学院中等部合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、とばすべき問題
問題別寸評
［１］
小数・分数の四則混合問題です。かけ算・わり算の時は分数に直し、足し算・引き算の時は小数に直して計算することを念頭に解き進めましょう。
［２］
［１］と同様、計算問題ですが、こちらは分数のみを扱う問題です。落ち着いて解けば必ず解ける問題です。
［３］
逆算の問題です。整数しか出てこない簡単な問題です。必ず得点すべき問題になります。
［４］
整数の条件付き問題です。問題の意味をしっかりと掴み、言われていることを式にすれば解ける問題です。算数の問題は、常に「取扱い説明書」だと思って、どういう操作をすればどうなるのかということを考えて読んでいきましょう。自分の考えや予想は時として必要ない場合があります。まずはしっかりと読む、理解するというスタンスが大切です。
［５］
簡単な比例の問題ですが、扱う数字が大きいので戸惑った受験生も多かったのではないでしょうか。普段から大きな数字の問題に慣れておく必要があります。ただ、単位が大きいというだけで、根本は［比例］です。「87万トン中84％が小麦になる」ということと、「１つのパンを作るのに250gの小麦粉が必要」ということを使って何個のパンが出来るかを求めます。
［６］
「国語のテスト」、「算数のテスト」、「平均点８０点以上」、「８０点未満」というように、問題に出てくるキーワードが多いので、どう整理していいか悩んだ生徒も多かったと思います。情報が多い場合いは、表、面積図、グラフ、ベン図などとにかく図を使って整理していきましょう。そうすると、意外と問われていることは簡単です。
［７］
もとになる直方体の体積をたて×横×高さ＝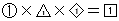
とすると、
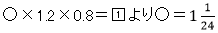となります。たての割合を求めてアの面積とイの面積を比べましょう。
［８］
ベン図の利用です。問題文は長いですが、長いということは情報を多く与えてくれているということなので、ベン図を描いて、問題文にある数値を埋めていきましょう。
［９］
比較的今年度の問題は、［比］のみで扱う問題が多かったように感じます。この問題も、ミカン、ナシ、リンゴの1個当たりの金額の比を求めて、リンゴ２６個の代金と同じになるということを表します。1個当たりの比がミカン：ナシ：リンゴ＝②：③：⑥なので、ナシとミカンの個数を□とすると、
□×2×②＋□×③＋□×⑥＝□×（④＋③＋⑥）＝⑥×２６個
□×①＝⑫となるので、□＝１２個
となります。よってミカンは２×１２＝２４個です。
このように、具体的な金額、個数が出ていなくても比のみで式をつくり求めることができます。ただ、やはり受験生は具体的な数値がないと、何が比で、何が具体的な数値なのかがわからなくなり、式さえも作れないという状況になってしまいます。とにかく、「根本」に戻って、「個数×１個分の値段＝代金」というこの式に持っていけるようにしましょう。割合と比を勉強する時に、比しか出てこない問題を意識して解かせるようにしてみてください。
［１０］
サイコロの性質を使う問題です。「向かい合う面の和が７」であるということは、受験生であれば皆知っているはずです。しかも問題に書いてくれています。A＋B＋C＝７、Cに当てはまる条件は、５の面が見えているのでそれ以外の面（３か４）（１か６）、AとBに当てはまる条件は、上の面に６が見えているので、Aが（２か５）のときにBは（３か４）であり、Aが（３か４）のときにBは（２か５）となります。始めのA＋B＋C＝７と合わせて場合分けをして考えていくと答えにたどり着きます。
［１１］
水の入っている容器に円柱を入れるという典型問題です。ここでは、半径の長さも高さも分かっていますが比を利用して解いた方が早いでしょう。
容器AとBの底面積の比は、半径の比が９：１５＝③：⑤なので、面積比＝⑨：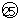
水の体積は13㎝入っているので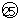×13＝325と表すことができます。
容器Aに容器Bを入れると底面積比は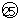−⑨＝16となり、16×17.5㎝＝280
325-280＝45 この体積分が容器Bの中に入ります。容器Bを引き上げた時に、その分だけ水の体積は減っているので、容器Aに残っている体積は280となります。その280を底面積で割れば容器Aの水の高さが求められます。280÷25＝11.2㎝・・・ア
容器Bの水の高さは、45÷9＝5㎝・・・イ
半径を実際使ってしまうと、計算に3.14が出てきてしまいます。体積ももちろん具体的な数値を求めることが出来ますが、結局底面積で割ると3.14は消えるので、始めから比で解いた方が楽です。その辺りを、問題を解く前に考えてから解き進めるようになると、スピードと正確性がアップしてきます。
［１２］
アの面積＝イの面積＋39㎠より、アを含む半径２０㎝の四分円と、イを含む台形EBCDの面積を求める式を作りましょう。こちらも典型問題です。受験生ならどこかで練習したはずです。必ず得点しておきたい問題です。
［１３］
三角数が変形した問題です。三角数は受験生なら必ずマスターしておきたい問題ですが、多くの生徒が苦戦する問題でもあります。合否を分けた一題で詳しく見ていきます。
［１４］
動く歩道、速さ、比の扱い、歩幅と歩数が絡んだ問題です。速さの比が出てくる場合、必ず、等しい部分を見つけてから解いて下さい。「速さ」が等しいのか、「道のり」なのか、「時間」なのか、この３つを考える必要があります。花子さんの移動する速さ＝動く歩道の速さとなることにも注意しましょう。
合否を分けた一題
２０１６年度の問題は、例年通り１２題〜１８題という枠の中に収まる問題数で、今年は14題でした。難易度もそれほど変化はなく、青山学院中等部を目指して過去問練習をしてきた受験生にとっては解きやすかったのではないかと思います。［１］〜［４］までの計算問題は、必ず得点しておきたい問題です。
また、比を扱う問題が多いのも特徴なので、青山学院中等部を目指すのであれば、［割合と比］の単元学習の時に、「速さと比」「物の値段と個数の比」など比だけで扱う問題も特に意識して練習しておく必要があります。その中で今年は、［１３］の数の性質の問題を取り上げます。数の性質のなかでも、扱いにくいのが三角数、四角数。なぜ扱いにくいかと言いますと、「数」のオンパレードだからです。数列ももちろん数ですし、何番目、何段目、すべて数ででてきます。当たり前なのですが、これが受験生を混乱させてしまうもとなのです。今何を自分は求めているのか、番号なのか、数列なのか、そこを意識して解いていく必要があります。
それでは、解説です。
この三角数は、奇数段目と偶数段目の数の並べ方が逆になるパターンです。
１段目 １
２段目 ３ ２
３段目 ４ ５ ６
４段目 10 ９ ８ ７
５段目 11 12 13 14 15
６段目 21 20 19 18 17 16
７段目 22 23 24 25 26 27 28
と続きます。
三角数の基本は「N段目の最後の数は求めることができる」ということです。
つまり、例えば、３段目の最後の数は、1＋2＋3＝6の「6」を求めることが出来ます。
また、この問題は、奇数段目は普通に「N段目の最後」をもとめ、偶数段目は、「N段目の最後」が一番左にくるということを使って解いていきましょう。
（１）２０段目は偶数段目なので、一段前の１９段目の一番最後を求めます。
２０段目の一番右は、１９段目の最後の数+１だからです。
（1＋19）×19÷2＝190←これが１９段目の最後の数つまり一番右
190＋1＝191
（２）250はどこにあるかを求める問題です。
まずは、250に近い「1〜Nまでの和」を見つけましょう。
20段目は、（1＋20）×20÷2＝210
21段目は、（1＋21）×21÷2＝231
22段目は、（1＋22）×22÷2＝253
よって、250は、22段目の中にあります。22段目は偶数段目なので、
左から、253、252、251、250、249、・・・・・と並んでいるので、
250は、22段目の左から４番目
三角数の基本的な問題ですが、意外と解きにくい問題です。並び方、基本の「1〜N番目までの和」ということを使えるようにする必要があります。こういう数の規則性の問題が出てくると、とにかくひたすら書いて解くという生徒がいますが、早いうちにその癖は治すようにしましょう。もちろん、いつか書いていけば正解するかもしれません。しかし、試験は時間も限られていてその中で正確に解く必要があります。一つの失点が大きく作用してしまうことが入試で多々あります。なので、確実に解けるように、速くて正確な「式」を利用して解くようにしましょう。それを日頃から意識して練習してください。
(まだ評価されていません)
Loading ...
青山学院中入試対策・関連記事一覧
青山学院中入試対策・同じ教科（算数）の記事
他校の同じ教科（算数）の記事
