算数の合否を分けた一題（2017年度）

算数の合否を分けた一題

慶應中等部入試対策・算数の合否を分けた一題（2017年度）

難易度分類

[１]	（１）A　（２）A　（３）A　（４）A
[２]	（１）A　（２）A　（３）A　（４）A
[３]	（１）A　（２）B　（３）B （４）B
[４]	（１）B　（２）B
[５]	（１）A　（２）B
[６]	（１）B　（２）C
[７]	（１）B　（２）C

Ａ：慶應中等部合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき

出題総評

今年も、例年通り大問7題構成となり、後半の問題になるにつれて難易度が上昇していく形式でした。また、解答欄に1ケタずつ数字を書く形式も踏襲されています。
大問１は計算を含む４問の小問集合、大問２は小問集合、大問３は図形分野の小問集合、大問４はダイヤグラムをテーマにした速さの問題、大問５はおもりを水中に沈める立体図形の問題、大問６は九九をテーマにした数の性質の問題、大問７は筆算をテーマにした数の性質と推理の問題、という構成でした。

問題別寸評

[１]

（１）

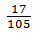
分数同士の四則演算。確実に通分して、計算ミスをしないようにしましょう。

（２）

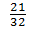
分数と小数の入り混じった穴あき算。こちらも、小数を分数にして一つ一つ丁寧に計算していくように。

（３）答　１８

じゃんけんをテーマにした場合の数の問題。４人のうち、1回で２人が勝つのは、勝った２人と負けた２人がそれぞれ同じ手を出した場合のみです。（グー２人・チョキ２人のように）
この問題も、本校の受験者としてはおさえなくてはなりません。

（４）答　２４

～を割ると～余る、という数の性質における約数が絡んだ典型題です。最も大きい数を聞かれているので、最大公約数をとった後に約数を調べる必要はありません。

[２]

（１）答　３．２

往復の平均の速さを求める問題。行きと帰りの時間が問題文で与えられているので、得点しなくてはならない問題です。

（２）答　１０

濃度の違う食塩水同志を混ぜ合わせる問題。面積図か天秤を使って、確実に正解しましょう。

（３）答　２７６０

お金の増減が絡む、割合の問題。太郎君と次郎君の情況を、問題文を読んでしっかりと式処理出来たかがカギです。次郎君のもとのお金を③円とおき、二人の残金を②円と考えるとスムーズに解けるでしょう。

（４）答　１０時３２分

ニュートン算の典型題。水そうの図を描けば、難なく処理できる問題です。

[３]

（１）

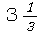
立体を切断して、表面積の増減を考えていく問題。1回切るごとに、もとの立方体の2面分の面積が増えることが分かっていれば、問題なかったでしょう。

（２）答　４０６

相似をテーマとした、長方形と三角形の求積問題。問題文から、長方形の縦の長さは２７ｃｍと分かりますが、図の右側にある底辺を２０ｃｍとした三角形の高さを求めるのに苦労した受験生はいると思われます。ピラミッド相似を使う点がカギです。

（３）答　４５

等しい長さに着目する、角度の問題。三角形DBCだけでなく、三角形DEFも直角二等辺三角形であることに気付けた受験生はすぐに答えが求まったでしょう。

（４）答　１４５６．９６

回転体をテーマにした、複雑な立体図形の表面積を求める問題。上から（円の面積）、まわりから（空洞になっている円柱の側面積＋全体の図形の側面積）、下から（円すいの側面積）と方向別にわけ、円周率３．１４の計算工夫を効率よくおこなうことで、時間の短縮となり後半以降の問題に手が回せます。

[４]

横軸を時間、縦軸を距離ではなく人の速さとしたダイヤグラムの問題。詳細は後述します。

（１）答　１１７０

（２）答　９１９０

[５]

おもりを水中に沈め、水面の上昇する高さや、容器を傾けた時の長さを考える立体図形の問題。

（１）

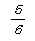
三角柱のおもりの体積を求め、容器の底面積で割ることによって答えが求まります。後半といえど、本校の受験生としては欠かせない問題です。

（２）

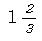
問題文で与えられている図２が少々分かりづらいが、どのように傾けたのかを問題文からイメージすることは容易かったと言えるでしょう。底面を台形PAEFと捉えることが出来れば、高さはFG＝２０ｃｍなので逆算によってPFも求まります。

[６]

九九の掛け算表をテーマにした、珍しい形式の数の性質の問題。最初に、表のマスをすべて埋めるところから始まります。

（１）答　１２

横に隣り合っている数を３つ並べているので、真ん中の数が平均になっていることに気付ければ、組の真ん中が２４÷３＝８以下になっている箇所を調べつくしていくだけです。

（２）答　３８

整理の方法と、そこからの調べ上げにかなりの時間を要する問題です。和が１５で割れる枠と２７で割れる枠を考えます。
まず、和が１５になる枠＝枠の真ん中が５になる組は、４・５・６の１組だけです。
和が３０になる枠＝枠の真ん中が１０になる組は、８・１０・１２と５・１０・１５の２組です。・・・・・・・・・といった形で、１５で割れるものについては和が１３５になるものまで調べていきます（最高が３６・４５・５４の組）。
２７で割れるものについては、和が２７・５４・８１・１０８・１６２・１８９・２１６まで調べていきます（１３５は、１５と２７の公倍数なので、既に１５の方でカウントしています。ちなみに、最高は６３・７２・８１の組）。
和が１５になるものは１５組、和が２７になるものは１０組となりますので、全体からそれらを引くことによって答えが求まります。

[７]

各桁がわからない４ケタの数同志を足し合わせたり、かけ合わせることでどのような数になるかを考える、推理がからんだ数の性質の問題。

（１）答　１２４９

千の位から順に見ていきます。Aを１とするとBは２…と考えていきますが、Dについては繰り上がりを考慮しなくてはならないことに注意しましょう（８ではない）。

（２）答　８２４６

最後の問題ということもあり、取っ掛かりが掴みづらいかなりの難問でした。ポイントは2点。ABCD×D（あるいはC、B、A）が５ケタの数にならなくてはいけないこと。また、D×Dの一の位がDであること。ここから、Dは１，５，６のどれかになりますが、ABCDは最小の数なので、一の位であるDは６とおいて考えていくことになります。それをふまえたうえで、一の位に着目するとC×６はC、B×６はB、A×６はAとなるのでA,B,Cは２，４，８のどれかに該当する、と考えていくことが出来ます。後は、先述した５ケタになるという観点からそれぞれの数で調整をしていくと答えが求まります。

合否を分けた一題

今年の慶應中等部の算数は、各単元がバランスよく出題されており、昨年と比較しても例年通りの難易度と言えますが、中では大問の６や７のように、あまり見慣れない形式の問題も目立ちました。そこで時間を浪費せずに、いかに４５分という短い時間の中で大問の５までに取り組めたかが合否の分かれ目だったと言えます。
今回は、前半の問題群の中で大問４のダイヤグラムの問題を、合否をわけた一題としてご紹介いたしましょう。

［４］速さとダイヤグラム

（１）

グラフの読み取りだけでなく、「電車が加速して一定の速さになる」という問題文の意味を正確に理解できたかが正誤の分かれ目です。
グラフの解読をしていきましょう。
０～６分は、太郎君が自転車（分速２８０ｍ）に乗ってA駅まで行く様子を表します。
６～１０分は、A駅で電車を待つ様子です。
１０～１３分は、電車に乗った後、だんだん加速して電車の速さが一定になるまでの様子を表しています。
１３～１８分は、一定の速さになった電車に乗っている様子です。
１８～２２分は、電車が目的地であるB駅につこうとしているので、だんだん減速していく様子を表しています。
２２～３３分は、B駅に着いた太郎君が分速８０ｍで歩いて学校に行く様子です。
この中で、１０～１３分に着目すると、最初は０ｍだった速さが、最終的には７８０ｍになりました。平均をとると（０＋７８０）÷２＝３９０ｍの分速でずっと進んだことと同じであることが言えます。よって、答えは３９０×（１３－１０）分＝１１７０ｍとなります。
答え：１１７０ｍ

（２）

（１）の意味が正確に捉えられれば、後はグラフのそれぞれの期間で距離を求めていくだけです。
０～６分⇒２８０×６＝１６８０ｍ
１０～１３分⇒（１）の答えから１１７０ｍ
１３～１８分⇒７８０×５＝３９００ｍ
１８～２２分⇒３９０×（２２－１８）分＝１５６０ｍ
２２～３３分⇒８０×１１＝８８０ｍ
よって、１６８０＋１１７０＋３９００＋１５６０＋８８０＝９１９０ｍとなります。
答え：９１９０ｍ

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？