算数の合否を分けた一題
豊島岡女子中入試対策・算数の合否を分けた一題（2017年度）
難易度分類
| １ | （１）Ａ （２）Ａ （３）Ｂ （４）Ａ/td> |
|---|---|
| ２ | （１）Ａ （２）Ｂ （３）Ａ （４）Ａ |
| ３ | （１）Ａ （２）Ａ |
| ４ | （１）Ａ （２）Ｂ （３）Ｂ |
| ５ | （１）Ｂ （２）Ｂ （３）Ｃ |
| ６ | （１）Ｂ （２）Ｃ |
Ａ：豊島岡女子合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題
出題総評
計算問題と一行問題が８問、大問４題の出題構成は例年通りです。点の移動の問題、立体図形の切断と少し難しめの問題が出題されています。ただし、基本的な問題も多く出題されていますので、どの問題を確実に解いていったかが合否のポイントとなりました。
問題別寸評
（１）
小数と分数の混じった四則計算です。確実に正解したいです。
（２）
カードを並べて4けたの偶数を作る、場合の数の基本問題です。
（３）
のべの量で考える仕事算の問題です。設定があまり目にかからないものでした。
（４）
単位換算を伴う割合の問題です。きちんと条件を整理して解きたい問題です。
（１）
1から14までかけた積が24で何回割り切れるかを求める数の性質の問題です。
24＝2×2×2×3であることに注意して、確実に正解したい問題です。
（２）
年令算の発展問題です。何年前かがわからないので、年令の差が変わらないという条件にどうやって結びつけるかがポイントです。
（３）
給水と排水を用いた仕事算です。数値が複雑ではありませんので、確実に正解したい問題です。
（４）
平面図形の面積の問題です。求めたい辺の長さに合わせて、相似形を使い分けられたかがポイントです。
（１）
食塩水の基本問題です。確実に正解しておきましょう。
（２）
（１）が正解できれば、Ｃの食塩水の量に関わらず、３つの食塩水を混ぜた濃さが6％になることがわかります。あせらずに解けたかがポイントです。
（１）
円の周りを移動する点の問題です。円の周りを移動するときは角速度で考えるという定石に従って解けば難しい問題ではありません。ただし、Ｏ、Ｐ、Ｑが初めて一直線になる状態が「Ｐ、Ｑ、Ｏ」の順ではなく「Ｐ、Ｏ、Ｑ」の順になることに気が付けたかどうかがポイントでした。
（２）
Ｏ、Ｐ、Ｑを結ぶ三角形が直角三角形になるときを考える問題です。これは気をつけたい問題で、どの角が直角になるかできちんと場合分けをする必要があります。類題を解いたことがあるかどうかが鍵となった、少し難しい問題でした。
（３）
180秒の間に何回直角三角形になったかを答える問題です。こちらも直角三角形になる状態がきちんとわかっていないと正解を求めることはできませんので、合否を分けた一題と言えるでしょう。
（１）
ボールを渡す規則を使った場合の数の問題です。全員が同じ個数持つ、という条件から、最初に箱を取る人が毎回異なると気づけたかがポイントです。
（２）
Ｅが１個しかボールを持っていないときのＣの持っているボールの個数を求める問題です。Ｅがボールを受け取れない状況を考えて調べられたかがポイントです。
（３）
ＡよりもＥが多くボールを持っている場合を考える問題です。この問題は状況を考えていくよりも、全ての組み合わせ（16通り）を調べたほうが速く正解にたどり着くことができます。豊島岡女子の場合の数の問題は、悩むよりも手を動かすほうが吉と出るタイプの出題が多いので、臨機応変に対応していくと良いでしょう。
（１）
正六角柱から三角すいを切り落とした立体の体積を求める問題です。同様の立体は、過去男子校の入試問題で出題されたことがあります。豊島岡女子を志望された受験生の多くは解いたことがなかったかもしれません。立体そのものがどうやって作られたのかを考え、そこから体積を求めていく思考が大切です。
（２）
（１）で求めた立体を底面に平行に切断し、その体積を求める問題です。かなりの難問で正解率は低かったものと思われます。こちらも立体そのものを考えるのではなく、その立体をどうやって作るのかと考える必要があります。
合否を分けた一題
豊島岡女子を攻略するには、基本レベルを確実に正解し、やや難しい図形問題をどこまで正解できたかが大切です。図形の折り返し、直角三角形の相似、影の作図、正多角柱の切断など、幅広い知識や解法を習得し、しっかり使いこなせるまで演習しておかないと、今後も高得点勝負になりやすい豊島岡女子の算数に対応できません。
今回は大問４を説明してまいります。
（１）円の周りを点が移動するときの速さは、１秒間に何度周ったか、という角速度で考えます。Ｐは360×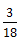
＝毎秒60°、Ｑは360×
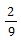＝毎秒80 °で進みます。
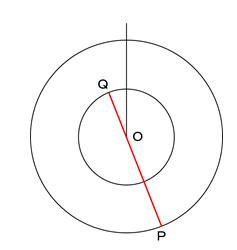
Ｏ、Ｐ、Ｑが初めて一つの直線の上に並ぶのは、下の図のようにＰとＱがＯをはさんで反対の位置に来たときです。
これは、角ＱＯＰ＝180°となったときとも言えます。
ＱはＰよりも毎秒20°多く進みますので、180÷20＝9秒後となります。
答え ９秒後
（２）三角形ＯＰＱが直角三角形になるときを考えます。角ＰＯＱが直角となるときがまず思いつくのではないでしょうか（下の図）。
しかし、この前に直角三角形になる瞬間があります。それは、角ＰＱＯが直角になるときです（下の図）。
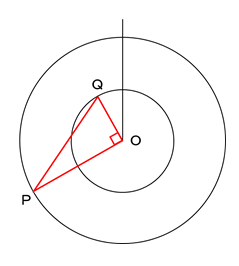
このとき、角ＰＯＱは何度になるでしょうか。
そのヒントは、２つの円の半径にあります。大きい円の円周が小さい円の円周の２倍なので、半径も２倍です。つまり、ＯＰ：ＯＱ＝２：１となっています。
ここで、角ＰＱＯが直角、ＯＰ：ＯＱ＝２：１という条件から、角ＰＯＱ＝60°と求められます（三角形ＰＱＯは正三角形を半分にした形）。
よって、ＱがＰより60°多く進んだときが初めて直角三角形になるときです。
それは、60÷20＝3秒後と求められます。
先ほどの角ＰＯＱが直角となるときが次に直角三角形となるときで、それは90÷20＝4.5
秒後と求められます。したがって、4.5－3＝1.5秒です。
答え １．５秒
（３）Ｐ、Ｑ、Ｏがこの順に再び一直線になるのは、ＱがＰより360°多く進んだときで、それは360÷20＝18秒後になります。
この18秒間の間で三角形ＰＱＯが直角三角形になるときを考えます。
１回目と２回目は（２）で求めました。３回目は角ＰＯＱが360－90＝270°となったときです。それは、270÷20＝13.5秒後です。
そして、４回目は角ＰＯＱが360－60＝300°となったときです。それは、300÷20＝15秒後です。
したがって、18秒間の間に４回直角三角形になります。
よって、180秒間の間では、（180÷18）×4＝40回直角三角形になります。
答え 40回
(3 votes, average: 2.67 out of 5)
Loading ...
豊島岡女子中入試対策・関連記事一覧
豊島岡女子中入試対策・同じ教科（算数）の記事
豊島岡女子中入試対策・同じテーマ（合否を分けた一題）の記事
- 理科の合否を分けた一題（2012年度）
- 算数の合否を分けた一題（2015年度）
- 国語の合否を分けた一題（2015年度）
- 国語の合否を分けた一題（2016年度）
- 社会の合否を分けた一題（2016年度）
- 算数の合否を分けた一題（2016年度）
- 理科の合否を分けた一題（2016年度）
- 国語の合否を分けた一題（2017年度）
- 理科の合否を分けた一題（2017年度）
- 社会の合否を分けた一題（2017年度）
- 算数の合否を分けた一題（2018年度）
- 理科の合否を分けた一題（2018年度）
- 国語の合否を分けた一題（2018年度）
- 社会の合否を分けた一題（2018年度）
- 社会の合否を分けた一題（2019年度）
- 算数の合否を分けた一題（2019年度）
- 理科の合否を分けた一題（2019年度）
- 算数の合否を分けた一題（2020年度）
- 社会の合否を分けた一題（2020年度）
- 国語の合否を分けた一題（2020年度）
- 理科の合否を分けた一題（2020年度）
- 算数の合否を分けた一題（2021年度）
- 国語の合否を分けた一題（2021年度）
- 社会の合否を分けた一題（2021年度）
- 理科の合否を分けた一題（2021年度）
他校の同じ教科（算数）の記事
